Because chords are constructed with stacked thirds, it’s important to know the intervals of thirds, and how to achieve them on the fretboard. First, let’s talk about the third intervals, then we’ll extend them to triads, and then to 7th chords.
There are exactly two types of thirds, termed major and minor. Large and small. That’s it. They are termed “thirds” because any diatonic scale contains 7 notes per octave, and the third note of that scale represents the third scale degree, making the distance (interval) between the root of the scale and the third scale degree, the interval of “a third.”
On a single string, you can count out the intervals from the root (termed the “unison” interval) to the minor 2nd, the major 2nd, to the minor 3rd and major 3rd. The thirds then span 4 and 5 semitones or half-steps or frets. If you think about the beginnings of a major or minor scale, these intervals stand out prominently.
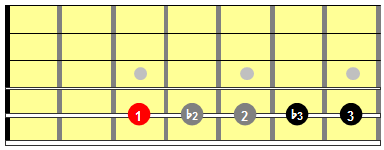
Figure 1: Single string major (3) and minor (b3) thirds
But to play the interval with both notes simultaneously, well need to find these notes across two different strings. Because the guitar is tuned in perfect fourths (with the exception of the B string…), moving up (in pitch) one string on the same fret produces a perfect 4th. It is easy to see, then, that the major 3rd is one semitone or half-step or fret lower; and the minor 3rd is two semitones or half-steps or frets lower.
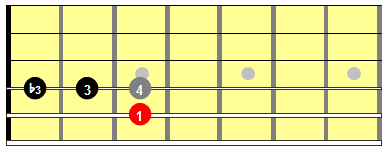
Figure 2: Adjacent string major (3) and minor (b3) thirds
The one exception is the interval that spans the G and B strings, as they are tuned to a major third interval naturally. So the same logic applies, just shifted one fret.
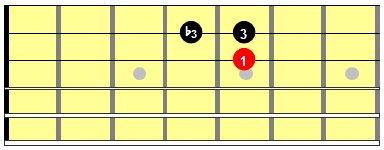
Figure 3: Adjacent string thirds across the G-B string tuning exception
Okay, there’s nothing overly exciting or overwhelming about these intervals of thirds. But the fact is, that’s nearly all there is to forming triads and extended chords. So let’s expand the discussion to triads.
Triads are formed by stacking two adjacent thirds on top of each other. We said earlier that there are only two types of thirds, major and minor. Therefore, a pair of thirds produces exactly four permutations of triads, enumerated below:
| Name | Stacked thirds construction | Spelling |
| Diminished | Minor 3rd + Minor 3rd = Diminished 5th | 1 – b3 – b5 |
| Minor | Minor 3rd + Major 3rd = Perfect 5th | 1 – b3 – 5 |
| Major | Major 3rd + minor 3rd = Perfect 5th | 1 – 3 – 5 |
| Augmented | Major 3rd + Major 3rd = Augmented 5th | 1 – 3 – #5 |
Now, since we already know how to construct these thirds, we simply do it twice, keeping in mind the exception created by the G-B string tuning.

Figure 4: Major 3rd (left) plus a minor 3rd (center) produces a Perfect 5th, and a major triad (right)
So the next time to need to form an augmented or diminished triad, there’s no need to fall back on memorization. Know that you understand the component thirds, you can reconstruct them on the fly with confidence:

Figure 5: Two major thirds stack to produce an augmented triad
Let’s next move these shapes across the fretboard, since the root can be placed on any of the six strings. Let’s simplify the example using just the major triads. From these, you can easily derive the minor, diminished, and augmented variants, right?
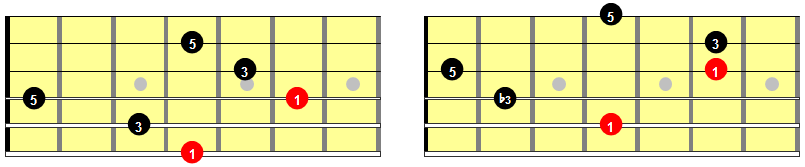
Figure 6: Major triad with roots on strings 6, 5, 4, and 3.
Now, when we reach the top two strings, we’re forced to play inversions of the triad, in which the root is no longer the lowest note of the triad. That’s okay, and in fact, the triads can be played in any inversion on the lower strings as well. To facilitate the inversions, remember that the distance (interval) between the root and the perfect fifth is by definition a fifth, and it’s inversion– the distance between a fifth and the next root (an octave above)– is a perfect fourth. For example, in C major (or minor) the G is a 5th above C, and a 4th below [the next] C. And since the guitar is tuned in perfect fourths, rising a fifth involves a string shift plus two frets, and lowering a fourth (rising a fifth!) involves only descending a string. You’ll also notice the familiar octave pattern of two strings and two frets between the two roots, the two 4ths, and the two 5ths, remembering to adjust for the tuning of the 2nd (B) string.
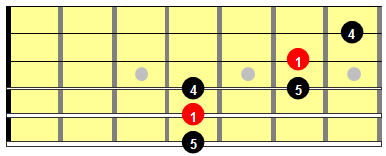
Figure 7: 5ths above (5) and below (4) the root conforming to the familiar octave pattern
[For completeness, the inversion of a diminished fifth is an augmented fourth, and the inversion of an augmented fifth is a diminished 4th. Ultimately, the two intervals sum to nine, as the note in the middle is effectively being counted twice. The inversion of a major interval produces a minor one; and vice-versa. So a major 3rd above C is the same note as a minor 6th below C, etc.]
So with this in mind, let’s get the root, 3rd and 5th of the major triads in place with the roots on strings 2 and 1.
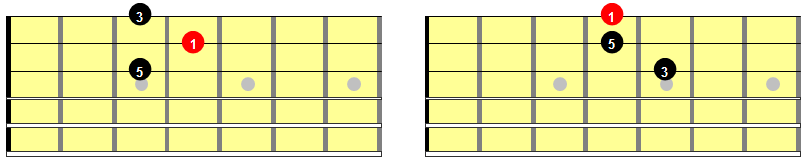
Figure 8: Major triads with roots on strings 2 and 1, necessitating „inversons“
Now, for sake of completeness, let’s use the octave patterns and 4ths/5ths to add notes to each major triad, doubling up one or more of the three existing notes an octave higher or lower. Note that even though there are more than three notes, these chords are still triads, as they are constructed only from the notes of the triad; the root, third, and fifth, of some quality.
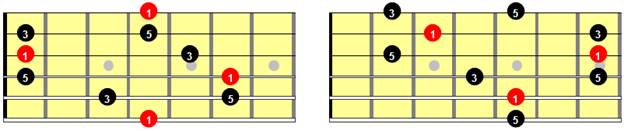
Figure 9: Extended major triads with roots on all strings
Do these patterns look familiar to you?
When the root of the chord (the root of the lower of stacked thirds) is on the 6th string, the pattern forms the beginnings of the G-shape barre chord. On the 5th string; the C-shape barre chord. The 4th string, the E-shape barre chord. And the 3rd; the A-shape barre chord. The 2nd; a D-shape barre chord. And the 1st? The top half of the G-shape barre chord. Makes sense, doesn’t it? These barre chords are simply triads extended across all six strings.
So now the next step– extending the triads to 7th chords.
What’s the formula? Same as it was before. Slap another 3rd on top. So taking the four types of triad, and adding either a major or minor third on top produces 8 possible permutations. Well, on five of them are commonly used in practice. It doesn’t make sense (and doesn’t sound good) to stack a major 3rd on top of a diminished triad, for example. Let’s enumerate the 7th chord formulas, and break them down into the stacked thirds:
| Name | Symbol | Stacked thirds construction | Spelling |
| Major 7th | M7 or Maj7 | Major/Minor/Major | 1, 3, 5, 7 |
| Dominant 7th | 7 or Δ7 | Major/Minor/Minor | 1, 3, 5, b7 |
| Minor 7th | m7 or min7 | Minor/Major/Minor | 1, b3, 5, b7 |
| Half-diminished 7th | Ø7 or min7b5 | Minor/Minor/Major | 1, b3, b5, b7 |
| Fully-diminished 7th | o7 or dim7 | Minor/Minor/Minor | 1, b3, b5, bb7 |
But now, whereas it was easy to follow the major and minor 3rd pattern on adjacent strings to produce three note triads, it’s not so trivial to add the fourth. That’d be quite a stretch for four notes.
So let’s take a closer look at the barre chords shapes. These are, in fact, triads that are easy to finger, for all but beginners. The most common of them are the E and A shapes, with the roots on the E and A strings, respectively. Each is spelled Root, 5th, Root (an octave above) and 3rd (an octave above). Then another 5th and root.
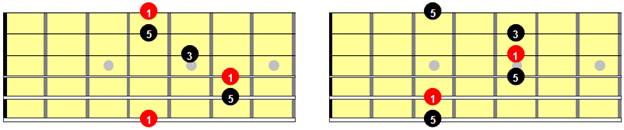
Figure 10: Barre chords with roots on the 6th (left) and 5th (right) strings
It’s really beneficial to know these intervals. Why? Because the one-and-only 3rd can be lowered a fret to produce a minor 3rd. And the the repeated root (an octave above) can be lowered one fret to form the major 7th, or two frets to form the minor 7th. Additionally, the perfect 5th can be altered to creat the diminished and augmented triads, although you’ll find it all but impossible to play more than 4 strings at a time, which is, of course, okay. Let’s diagram these adjustments for non-diminished versions containing the perfect 5th:
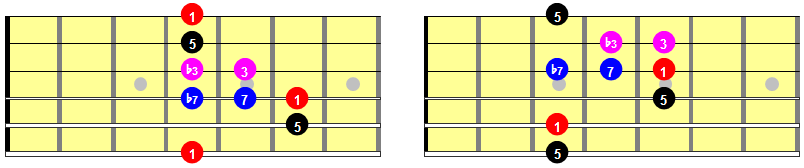
See all of the relationships? Major triads, minor triads, major 7ths, minor 7ths, and dominant 7ths all in one-stop shopping. Further they offer the adjustments necessary to form the diminished and augmented triads, as well as the diminished 7ths.
I won’t go into further extending these chords into 9ths, 11ths, and 13ths, as this article is long enough already… But just know that all of them still follow the original premise of stacking up intervals of major and minor 3rds.
About the author: Matt Fienberg is a guitarist and guitar teacher in Central Massachusetts. If you liked this article, please visit his website at ROI Guitar Studio, and be sure to let him know! He is available for comments, questions, and/or lessons, if you happen to be in his area!
